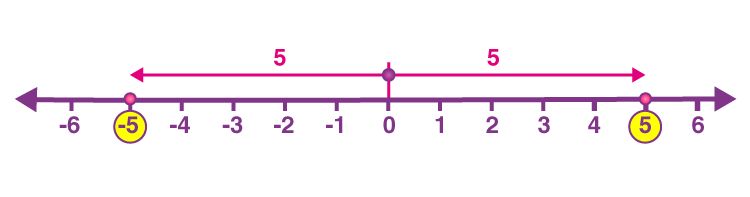
Modulul unui număr real reprezintă valoarea absolută a acelui număr, adică distanța pe axa numerelor de la origine până la numărul respectiv. Pentru că distanța este o valoare pozitivă, așa și valoarea absolută a unui număr înseamnă o valoare pozitivă. Astfel, valoarea absolută a două numere opuse este aceeași, adică | +7 | = | -7 | = 7.
Așa cum se vede mai sus, notația pentru valoarea absolută a unui număr este punerea numărului între două bare. Indiferent dacă un număr este negativ sau nenegativ (pozitiv), modulul va fi un număr pozitiv. Iar acest fapt nu necesită prea multe detalieri în acest articol. Dar, pentru că modulul unui număr este o valoare pozitivă, ce se întâmplă când spunem că | x | = 7? Ce valoare putem spune că are x? Ne punem altfel întrebarea: „modul din ce număr este egal cu 7?” Răspunsul, din nou, se află la finalul primului paragraf. Deci x poate fi +7 sau -7.
Haideți să scriem o altă ecuație cu modul: | x + 9 | = 20. Lucrurile încep să se complice, dar doar așa ni se pare. Pentru a nu ne încurca, putem să atribuim o altă literă pentru a înlocui tot ce este în interiorul modulului. adică x + 9 = y. Deci rescriem | y | = 20. Așa cum am văzut mai sus, y poate fi +20 sau -20. Deci avem cele două cazuri:
Cazul I: x + 9 = 20 x = 20 – 9 x = 11
Cazul II: x + 9 = – 20 x = – 20 – 9 x = – 29
Să mai rezolvăm o ecuație cu modul: | x – 3 | = 1. Fără a mai face înlocuirea lui x – 3 cu o altă literă, trecem direct la cazurile ecuației:
Cazul I: x – 3 = 1 x = 4
Cazul II: x – 3 = -1 x = – 1 + 3 x = 2
Pentru a face lucrurile mai interesante, rezolvăm o ecuație cu modul dublu, iar dacă prezintă interes voi reveni și cu alte astfel de ecuații. Din Caietul pentru vacanță de vară de clasa a VII-a de la Editura ART, pagina 42, luăm ecuația
| 15 – | 2x + 1|| = 8. Pare complicat, dar luăm treptat ecuația, pe cazuri. Mai întâi ne ocupăm de modulul exterior:
Cazul I: 15 – | 2x + 1| = 8 | 2x + 1| = 15 – 8 = 7
De aici se ramifică în două cazuri distincte: Cazul I a) 2x + 1 = 7 2x = 6 x = 3; Cazul I b) 2x + 1 = -7 2x = -8 x = -4
Revenim la modulul exterior și scriem Cazul II: 15 – | 2x + 1| = -8 | 2x + 1| = 15 – (-8) | 2x + 1| = 15 + 8 = 23
Cazul II a) 2x + 1 = 23 2x = 23 – 1 = 22 x = 22 : 2 x = 11, și
Cazul II b) 2x + 1 = – 23 2x = – 23 – 1 2x = – 24 x = – 24 : 2 x = – 12
Deocamdată atât, revin cu alte proprietăți ale modulului dacă vor prezenta interes.